GCN阅读笔记

April 2, 2023, 1:20 PM

作者的研究目标是什么？

图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡，关系越亲近的邻居影响越大。

Background

卷积定理：函数卷积的傅里叶变换是函数傅里叶变换的乘积，即对于函数与两者的卷积是其函数傅里叶变换乘积的逆。

将传统的傅里叶变换和卷积迁移到Graph上，

得到最原始的图卷积公式

深度学习中的Convolution就是要设计含有trainable共享参数的kernel,从（1）可以看出:graph convolution中的卷积参数就是

第一代GCN

Sepctral Networks and Locally Connected Networks on Graphs

简单粗暴直接将变成了卷积核，即layer为，其中：

弊端：

（1）每次前向传播，计算三个矩阵的乘积，对于大规模的graph，计算代价高，复杂度为O（）；

（2）卷积核不具有spatial localization，即对于节点位置不敏感；

（3）卷积核需要n个参数

第二代GCN

Convoutional Neural Networks on Graphs with Fast Localized Spectral Filtering

将设计成，即layer为，其中：

layer可以变成：

优点：

（1）卷积核只有K个参数，一般K远小于n，参数的复杂度大大降低；

（2）矩阵变换后，不需要特征分解，直接用拉普拉斯矩阵L进行变换，需要计算

,计算复杂度仍是;

(3)卷积核有很好的spatial localization，K就是卷积核的接受域receptive field。

第三代GCN

其中（1）的计算量很大，因为特征向量矩阵的复杂度是。另外对于大型图来说，的特征值分解的计算量很大。为了解决这个问题，Wavelets on graphs via spectral graph theory论文提出了可以很好地通过Chebyshev多项式的阶截断展开来拟合。

利用chebyshev多项式代替卷积核，

是re-scaled的特征值对角矩阵，，因为切比雪夫多项式输入在[-1,1]之间。

带入中可得：
将矩阵运算放在多项式内，
因为拉普拉斯矩阵，代入可得：

}

其中。

好处:计算过程无需对拉普拉斯矩阵进行特征分解，最大特征值可以用幂迭代法求出，也无需进行特征分解。

💙

为了简化模型，取一阶chebyshev，拉普拉斯最大特征值，

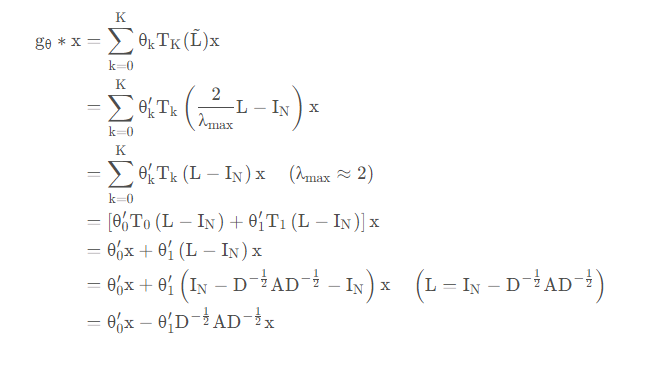
得到：

💙

进一步限制参数数量，解决过拟合问题，为可训练的自由参数。

则有：

其中特征值范围在[0,2]之间，如果深度神经网络使用这个算子，会导致梯度爆炸/消失。

💙

采用==renormalization trick==（归一化技巧），使它的特征值落在[0,1]范围中，

其中，，即图中加上自环。

每层图卷积正式定义为：

，其中

推广到具有C个输入通道（即每个节点有C维特征向量）的信号和个滤波器或特征映射：

其中，

Method

结合了一阶Chebyshev、运用了拉普拉斯矩阵特性、进行了renormalization trick、叠加多层GCN。

前向传播形式

由于是用来一阶切比雪夫多项式，想要获得更高阶邻居信息，可以叠加多个卷积层，论文中作者是用了两层GCN，由上一节可得前向传播形式：

其中,可以通过预处理进行计算，对于卷积网络中的AXW可以理解为：A代表传播propagation聚合邻居信息，W代表转换transformation改变特征维度、特征增强。